2. Principal Stresses and Principal Strains in Civil Engineering (Strength of Materials)

 

Principal Stresses and Principal Strains in Civil Engineering (Strength of Materials)

Principal stresses and strains are fundamental concepts in mechanics of materials, particularly important in civil engineering for analyzing structures under complex loading (e.g., beams, columns, pressure vessels).

1. Principal Stresses

Definition: Principal stresses are the maximum and minimum normal stresses at a point in a stressed body. They act on principal planes where the shear stress is zero.

There are three principal stresses in 3D: σ₁ (maximum), σ₂ (intermediate), σ₃ (minimum). Convention: σ₁ ≥ σ₂ ≥ σ₃.

In plane stress (common in civil engineering, e.g., thin plates), one principal stress is zero (usually σ₃ = 0).

2. Formulas for Plane Stress (2D State)

Given stresses: σ_x (normal in x-direction), σ_y (normal in y-direction), τ_xy (shear).

Principal stresses (σ₁ and σ₂):

$$\sigma_{1,2} = \frac{\sigma_x + \sigma_y}{2} \pm \sqrt{ \left( \frac{\sigma_x - \sigma_y}{2} \right)^2 + \tau_{xy}^2 }$$

Maximum shear stress (τ_max):

$$\tau_{\max} = \sqrt{ \left( \frac{\sigma_x - \sigma_y}{2} \right)^2 + \tau_{xy}^2 }$$

(Note: In-plane max shear is half the difference of principal stresses: τ_max = (σ₁ - σ₂)/2)

Direction of principal planes (angle θ_p from x-axis):

$$\tan 2\theta_p = \frac{2\tau_{xy}}{\sigma_x - \sigma_y}$$

θ_p gives the orientation; the two planes are 90° apart.

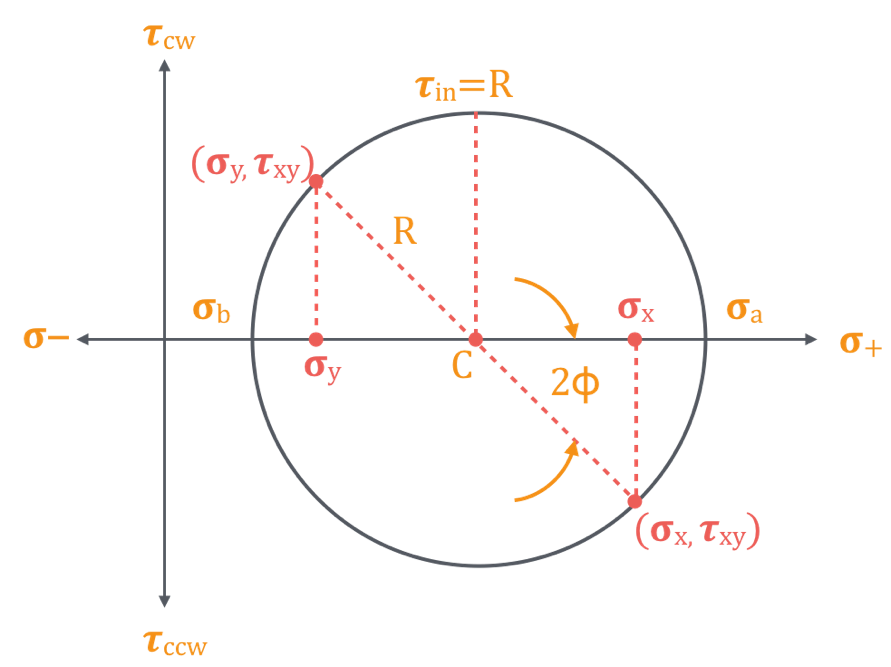
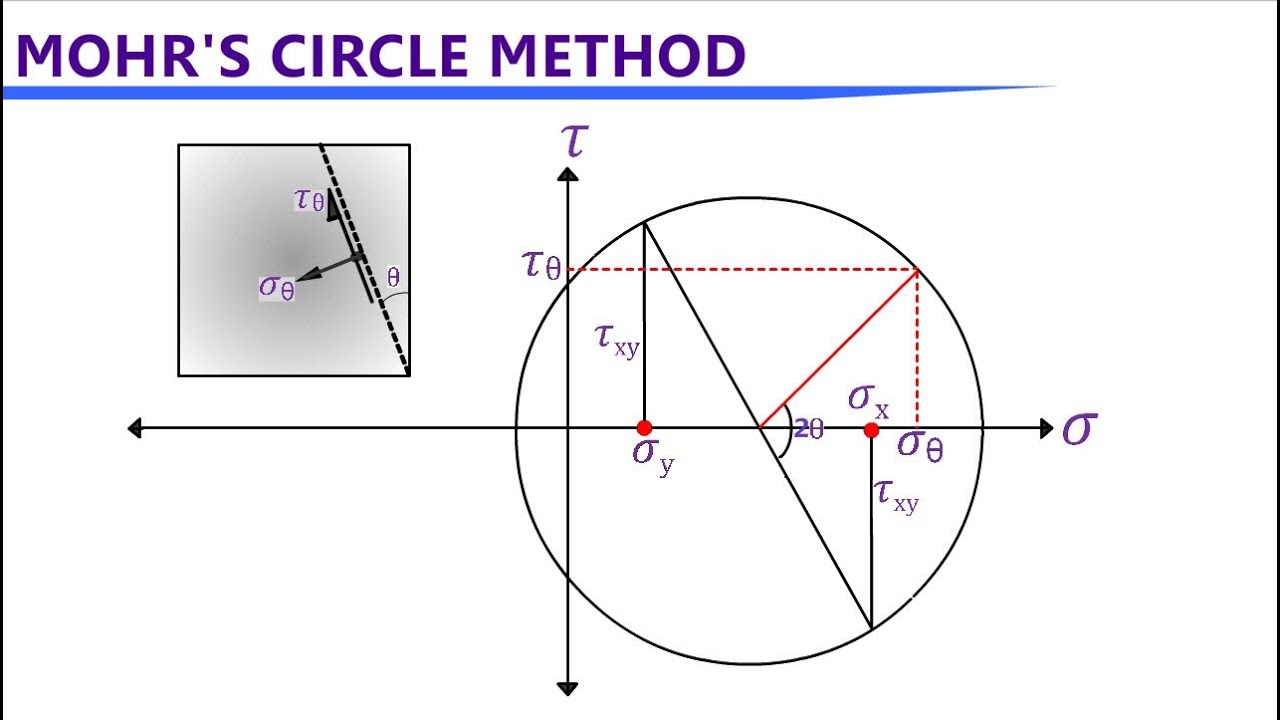
3. Mohr's Circle for Stress

Mohr's circle is a graphical method to find principal stresses, max shear, and stresses on any plane.

Construction:

• Plot normal stress (σ) on x-axis (tensile positive).
• Plot shear stress (τ) on y-axis (sign convention: often clockwise positive in some texts, but consistent).
• Center of circle: at average stress ($\sigma_{avg} = \frac{\sigma_x + \sigma_y}{2}$).
• Radius: $\sqrt{ \left( \frac{\sigma_x - \sigma_y}{2} \right)^2 + \tau_{xy}^2 }$.
• Points: (σ_x, τ_xy) and (σ_y, -τ_xy).

Principal stresses: intersections with σ-axis. Max shear: top/bottom of circle. Angle on circle is 2θ (double the physical angle).

For 3D, there are three Mohr's circles between the principal stresses.

4. Principal Strains

Definition: Similar to stresses, principal strains are maximum and minimum normal strains, on planes of zero shear strain.

In isotropic linear elastic materials, principal strain directions coincide with principal stress directions.

Formulas (analogous to stress):

$$\epsilon_{1,2} = \frac{\epsilon_x + \epsilon_y}{2} \pm \sqrt{ \left( \frac{\epsilon_x - \epsilon_y}{2} \right)^2 + \left( \frac{\gamma_{xy}}{2} \right)^2 }$$

Where γ_xy is engineering shear strain (not tensor γ/2).

Mohr's circle for strain: Similar construction, but use γ_xy/2 for the shear coordinate.

Mohr circle for strain. 

5. Relation Between Stress and Strain (Hooke's Law - Plane Stress)

For isotropic material:

$$\epsilon_x = \frac{1}{E} (\sigma_x - \nu \sigma_y), \quad \epsilon_y = \frac{1}{E} (\sigma_y - \nu \sigma_x), \quad \gamma_{xy} = \frac{2(1+\nu)}{E} \tau_{xy}$$

Principal strains from principal stresses:

$$\epsilon_1 = \frac{1}{E} (\sigma_1 - \nu \sigma_2), \quad \epsilon_2 = \frac{1}{E} (\sigma_2 - \nu \sigma_1)$$

(In plane strain, ε_z = 0, relations differ.)

6. Applications in Civil Engineering

• Failure theories: Maximum principal stress theory (Rankine) for brittle materials like concrete.
• Thin-walled pressure vessels: Hoop and longitudinal stresses are principal.
• Strain rosettes: Measure strains at different angles to find principal strains/stresses.
• Soil mechanics: Mohr-Coulomb failure criterion uses Mohr's circle.