7. Columns and Struts in Strength of Materials (SOM) - Civil Engineering

 

Columns and Struts in Strength of Materials (SOM) - Civil Engineering

In Strength of Materials (SOM), columns and struts are structural members subjected primarily to axial compressive loads. Failure can occur by crushing (for short members) or buckling (lateral instability for slender members). Understanding buckling is crucial in civil engineering for designing safe columns in buildings, bridges, and frames to prevent sudden collapse.

Definitions

• Column: A vertical structural member transmitting compressive loads from beams/slabs to foundations (e.g., RCC or steel columns in buildings).
• Strut: Any inclined or horizontal compression member (e.g., in trusses, bracing systems). The analysis is similar to columns.

Both fail by:

• Direct compression (short members).
• Buckling (slender members) – sudden lateral deflection when load reaches critical value.

Types of Columns Based on Slenderness Ratio (λ = L_e / r)

• Short Column: λ < ~40–50 (fails by crushing; stress = P/A ≤ allowable compressive stress).

• Intermediate Column: Medium λ (failure by combination of crushing and buckling; uses empirical formulas like Johnson’s parabolic).
• Long/Slender Column: λ > ~80–100 (fails by elastic buckling; Euler's theory applies).

Euler's Buckling Theory (for Long Columns)

Assumptions: Perfectly straight, homogeneous, elastic, axial load, small deflections.

Critical buckling load (P_cr):

$P_{cr} = \frac{\pi^2 E I}{(L_e)^2}$

where:

• E: Modulus of elasticity
• I: Minimum moment of inertia
• L_e: Effective length = K × L (L = actual length)
• K: Effective length factor depending on end conditions

Critical stress: $\sigma_{cr} = \frac{P_{cr}}{A} = \frac{\pi^2 E}{(L_e / r)^2}$ (r = radius of gyration)

End Conditions and Effective Length Factor (K)

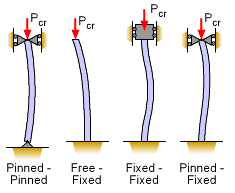
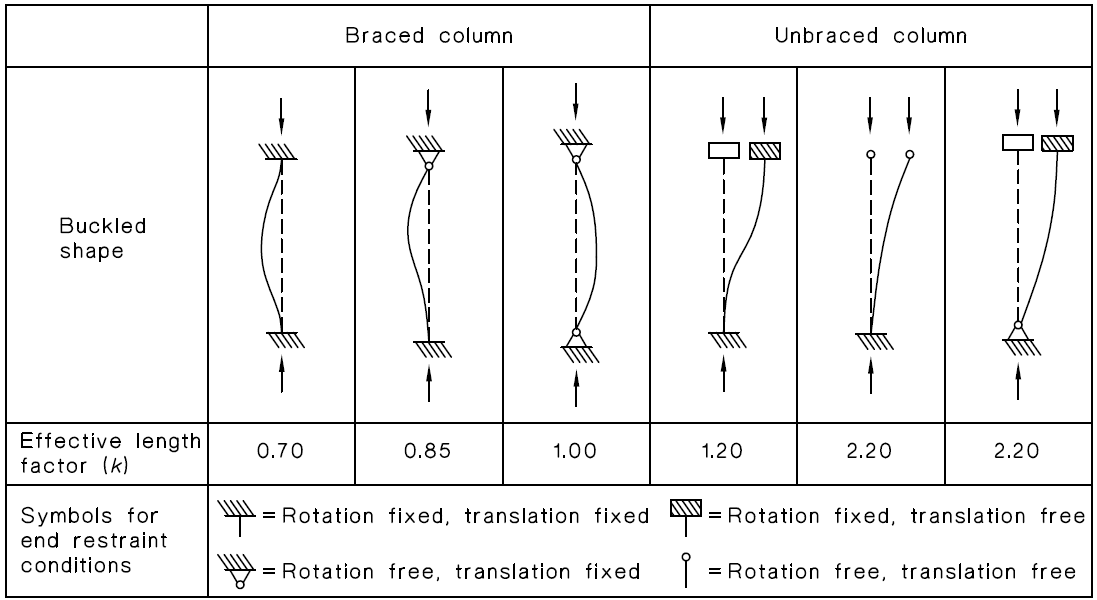
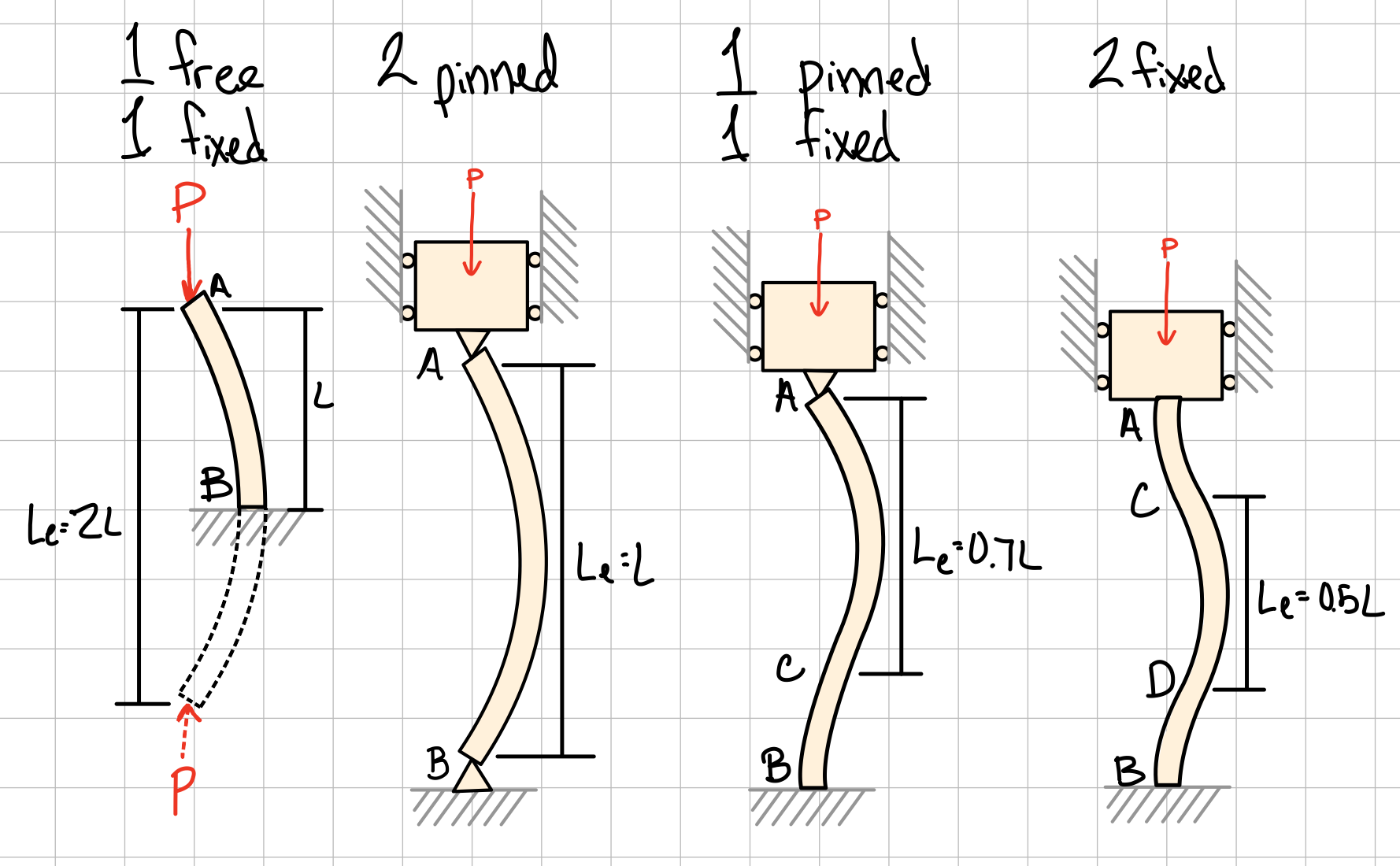
End Conditions	Theoretical K	Recommended K (IS 456/ AISC)	L_e	Buckling Mode
Both ends pinned (hinged)	1.0	1.0	L
Both ends fixed	0.5	0.65	0.65L
One fixed, one free (cantilever)	2.0	2.0	2L
One fixed, one pinned	0.707	0.80	0.8L

Limitations of Euler's Theory

• Valid only for long columns (high λ where σ_cr < yield stress).
• Assumes ideal conditions; real columns have imperfections → use factor of safety or reduced loads.

For short/intermediate: Use Rankine’s formula, Johnson’s formula, or code-based empirical relations.

Struts in Practice

• In trusses/bracings, struts carry compression; design for buckling using same Euler/Rankine formulas.
• End conditions often pinned → K ≈ 1.0.

In civil design codes (e.g., IS 456 for concrete, IS 800 for steel), columns are classified by slenderness, and permissible stresses are reduced for buckling. Always ensure P_actual < P_cr / Factor of Safety.

These concepts prevent catastrophic failures like buckling-induced collapse in structures. Refer to textbooks like R.K. Bansal or S. Ramamrutham for detailed derivations and examples.