8. Torsion , Spring , Pressure Vessels in Strength of Materials (SOM) - Civil Engineering

 

Torsion in Strength of Materials (SOM) - Civil Engineering

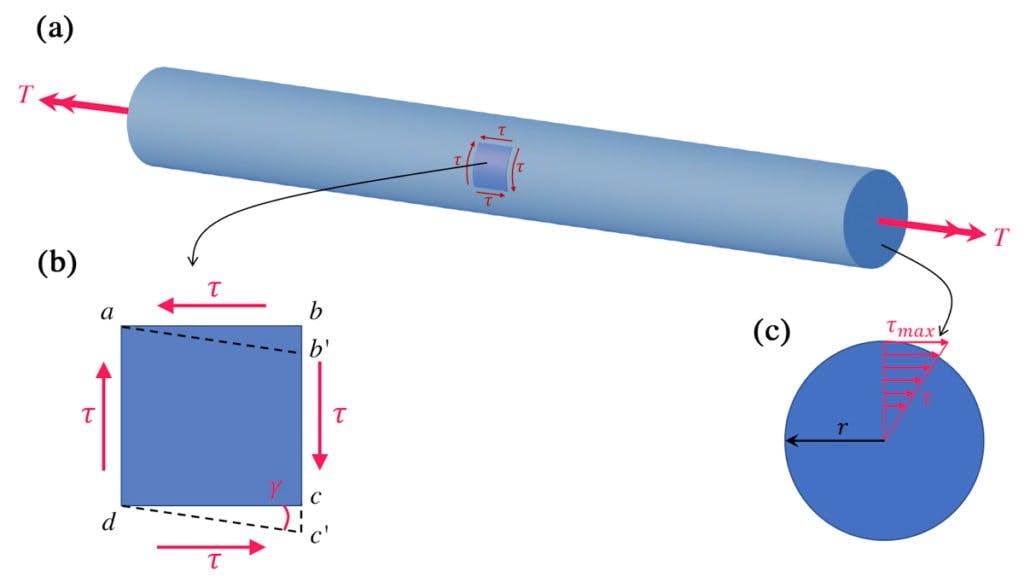
Torsion refers to the twisting of a structural member (usually shafts) subjected to torque (T) about its longitudinal axis. In civil/mechanical engineering, it's critical for designing shafts in machines, propeller shafts, or helical springs.

Assumptions (for Circular Shafts)

• Material is homogeneous and isotropic.
• Plane sections remain plane (no warping in circular sections).
• Radius remains straight.

Key formulas for solid/hollow circular shafts:

Shear stress (τ) at radius r:

$\tau = \frac{T \cdot r}{J}$

where:

• T: Applied torque
• J: Polar moment of inertia (J = πd⁴/32 for solid; π(D⁴ - d⁴)/32 for hollow)
• Max τ at outer radius (r = d/2)

Angle of twist (θ) in radians:

$\theta = \frac{T L}{G J}$

where:

• L: Length
• G: Shear modulus (modulus of rigidity)

Power transmitted: P = 2πN T / 60 (N in rpm)

Non-circular sections (e.g., rectangular) use different approaches like membrane analogy or Prandtl's stress function.

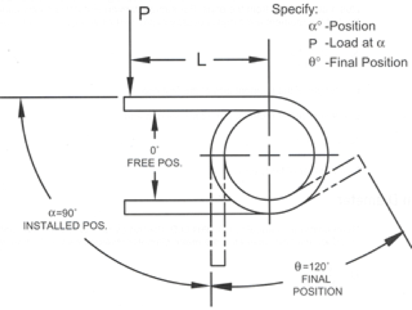
Torsion Springs (Helical Torsion Springs)

Torsion springs store energy by twisting (unlike compression/extension springs). Common in civil/mechanical applications like door hinges, garage doors, or automotive suspensions.

• They exert torque proportional to angular deflection.
• Made from wire (usually circular cross-section) coiled into helix.

Key formulas:

Deflection (angular, θ in radians):

$\theta = \frac{T L}{E I} + \frac{T L}{G J}$ (but primarily bending for close-coiled)

For helical torsion springs, stress is mainly bending stress (not pure torsion), but shear from torsion is considered with Wahl factor for stress concentration.

Max bending stress:

$\sigma = \frac{32 M}{\pi d^3} K_w$

(where M = torque × arm, K_w = Wahl correction factor)

Spring rate (k): Torque per radian deflection.

Design considers fatigue, surge, and buckling.

Pressure Vessels in SOM - Civil Engineering

Pressure vessels (boilers, gas cylinders, pipelines) contain fluids under pressure, developing hoop (circumferential), longitudinal (axial), and radial stresses.

Thin-Walled Pressure Vessels (t/d ≥ 20, where t = thickness, d = diameter)

• Radial stress neglected (≈0).
• Assumes uniform stress across thickness.

For Cylindrical Vessel (internal pressure p, diameter d, length L):

• Hoop stress (σ_h): $\sigma_h = \frac{p d}{2 t}$
• Longitudinal stress (σ_l): $\sigma_l = \frac{p d}{4 t}$
• Hoop is twice longitudinal → governs design.

Vessel:

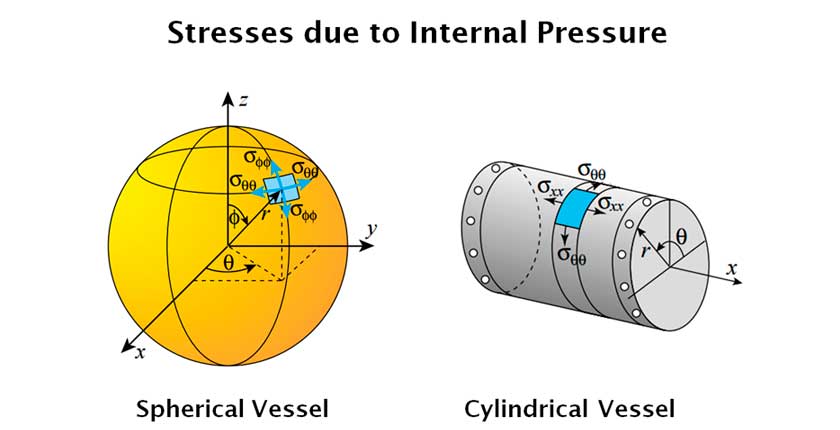
• Hoop stress (both directions): $\sigma_h = \frac{p d}{4 t}$
• More efficient (half the stress of cylinder for same p, d, t).

Thick-Walled Pressure Vessels (t/d < 20)

• Use Lame's theory (radial and hoop vary across thickness).
• For internal pressure p_i, external p_o=0:

Hoop stress: $\sigma_h = \frac{p_i r_i^2}{r_o^2 - r_i^2} \left(1 + \frac{r_o^2}{r^2}\right)$

Radial stress: $\sigma_r = \frac{p_i r_i^2}{r_o^2 - r_i^2} \left(1 - \frac{r_o^2}{r^2}\right)$

• Max hoop at inner surface; radial = -p_i at inner.

In design codes (ASME, IS 2825), factor of safety, joint efficiency, and corrosion allowance are applied. Failure theories (e.g., max shear for ductile) are used.

These topics ensure safe design against twisting failure or bursting in structures. Refer to SOM textbooks like R.K. Rajput or Beer & Johnston for derivations and problems.