6. Slope and Deflection of Beams in Strength of Materials (SOM) - Civil Engineering

 

Slope and Deflection of Beams in Strength of Materials (SOM) - Civil Engineering

In Strength of Materials (SOM), a core subject in civil engineering, the study of slope (rotation) and deflection (vertical displacement) of beams under loading is essential for ensuring structural safety, serviceability, and limiting excessive deformation (e.g., to prevent cracking in concrete or discomfort in floors).

Definitions

• Deflection (δ or y): The vertical displacement of a point on the beam from its original position.
• Slope (θ): The angle (in radians) that the beam's elastic curve makes with the original axis at a point. It is the rotation of the cross-section.
• The deformed shape of the beam centerline is called the elastic curve.

The fundamental relationship from Euler-Bernoulli beam theory is:

$EI \frac{d^2 y}{dx^2} = M(x)$

where:

• $E$: Modulus of elasticity
• $I$: Moment of inertia
• $M(x)$: Bending moment at distance $x$
• $EI$: Flexural rigidity

Integrating once gives slope: $EI \frac{dy}{dx} = \theta(x)$

Integrating twice gives deflection: $EI y = \delta(x)$

Common Methods to Calculate Slope and Deflection

1. Double Integration Method: Express $M(x)$, integrate twice, apply boundary conditions (e.g., y=0 at supports) to find constants.
2. Macaulay's Method: Extension of double integration using singularity functions for discontinuous loads (point loads, varying distributed loads). Uses bracket terms <x-a> that are zero when x < a.
3. Moment-Area Method:
   • Theorem 1: Change in slope between two points = area under M/EI diagram between them.
   • Theorem 2: Deflection at a point relative to tangent at another = moment of M/EI area about the point.
4. Conjugate Beam Method: Create a "conjugate" beam loaded with M/EI diagram.
   • Shear in conjugate = slope in real beam
   • Moment in conjugate = deflection in real beam
   • Supports adjusted (e.g., simply supported real → free end conjugate becomes fixed).

These methods are used for determinate beams; for indeterminate, additional techniques like slope-deflection are applied.

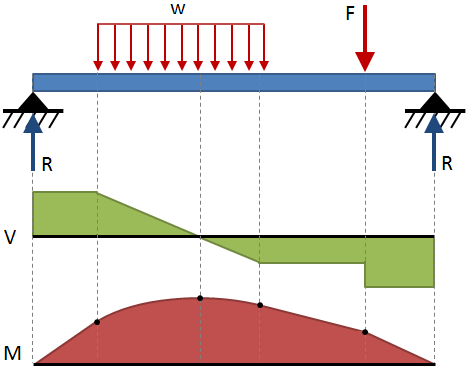
Standard Formulas for Common Cases

Here are typical diagrams and formulas for frequent loading cases (assuming constant EI, downward positive deflection).

Simply Supported Beam with Central Point Load P

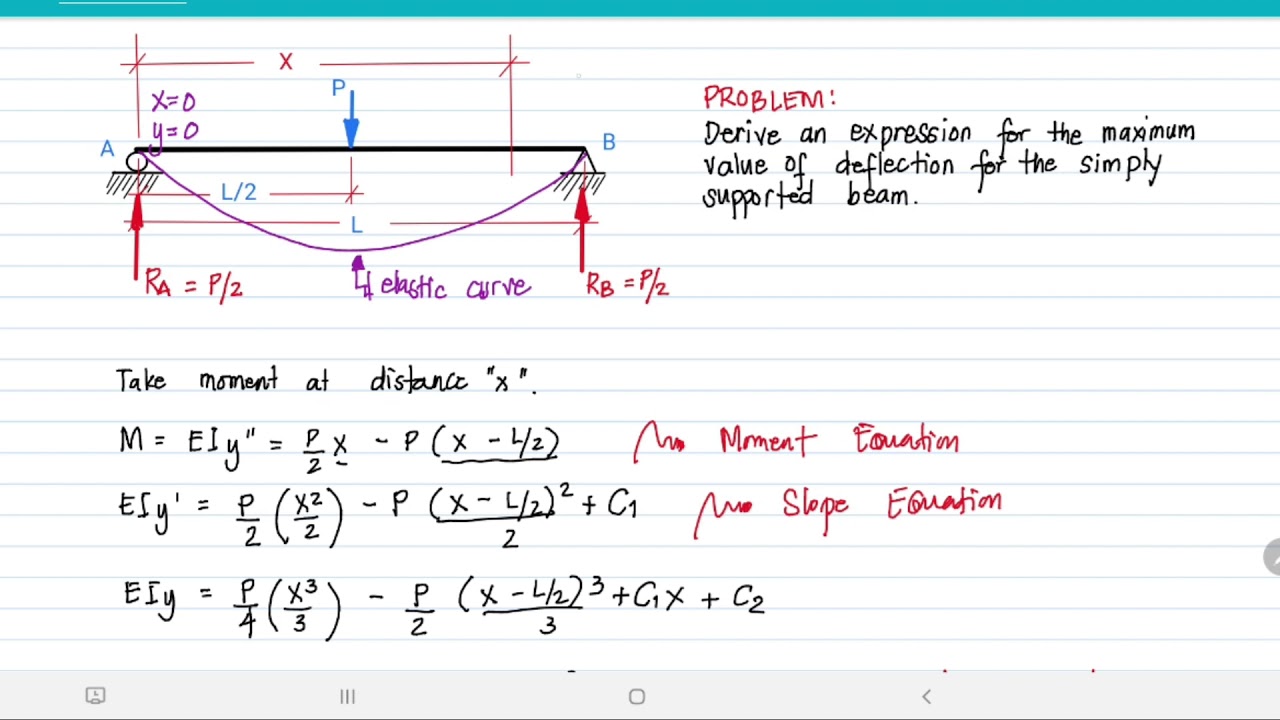
• Max deflection (at center): $\delta = \frac{P L^3}{48 EI}$
• Slope at ends: $\theta = \frac{P L^2}{16 EI}$

Cantilever Beam with Uniform Distributed Load (UDL) w

• Max deflection (at free end): $\delta = \frac{w L^4}{8 EI}$
• Slope at free end: $\theta = \frac{w L^3}{6 EI}$

For more cases (e.g., point load at any point, partial UDL), refer to standard tables in SOM textbooks like R.K. Bansal or Timoshenko.

These concepts are critical in civil engineering design codes (e.g., IS 456 for RCC limits deflection to span/250). Excessive deflection can lead to serviceability failures even if strength is adequate.